How to make a simple FM synthesizer

The final product

This is the simple FM synthesizer I made in javascript. Sure it lacks all the modern features commercial FM synthesizers have, but it's enough for a showcase. The source code belongs to public domain, in case you need it.

The math behind the formulas

The maths I used are taken from this paper. All the variables are explained thoughly in the paper except for time t which is range [0..1]. We will work with the final formula: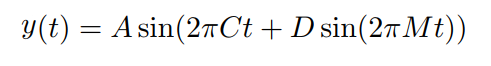

C Carrier frequency or pitch or fundamental frequency
D Depth of modulation or modulation power
M Frequency of modulator
t Range [0..1]. I substitute t with (i/sampleRate) which gives the instant in seconds since start of the sound.

This formula works perfectly for cases of a single modulator:

 
            
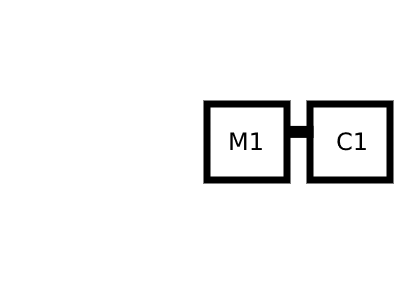
// Modulator M1 modulates C1    
return formulaValues.A1*Math.sin( 2*Math.PI*formulaValues.C1*(i/sampleRate) + formulaValues.D1*Math.sin(2*Math.PI*formulaValues.M1*(i/sampleRate)) );

The nested modulation (i.e. Modulator M2 modulates modulator M1 that modulates Carrier C1) is solved in the following way:

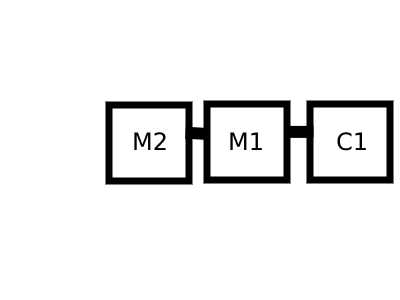Look at formula y(t)=A*sin(2*PI*C*t + D*sin(2*PI*M*t)). The final part (D*sin(2*PI*M*t)) is the formula of the amplitude of a sinusoidal wave of frequency M. That means this is where we plug the amplitude of M2 that is modulating M1.

 
            
let M1Ampl= 1 * Math.sin( 2*Math.PI*formulaValues.M1*(i/sampleRate) + formulaValues.D2*Math.sin(2*Math.PI*formulaValues.M2*(i/sampleRate)) );
return formulaValues.A1*Math.sin( 2*Math.PI*formulaValues.C1*(i/sampleRate) + (formulaValues.D1*M1Ampl) );

Now the operator feedback.

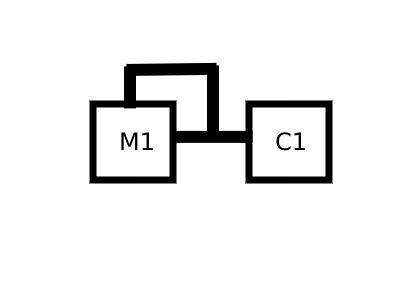
This case is solved simply saving the current value of the operator in a variable that we will use in the next iteration of the algorithm. Look at this code:

 
            
let M1Ampl= formulaValues.D1 * Math.sin( (2*Math.PI*formulaValues.M1*t) + (formulaValues.D1*window.oldC1Amplitude) );
window.oldC1Amplitude=M1Ampl; // we need the old value of M1 Amplitude to get the next new value
        
return formulaValues.A1*Math.sin( (2*Math.PI*formulaValues.C1*t) + (formulaValues.D1*M1Ampl) );

As you can see, at time t, M1 is modulated by its own former value, while the current value of M1 amplitude is saved in a variable that will be used at time t+1.